Comparación de medias – Dos grupos

En ocasiones los neuropsicólogos están interesados en conocer si las puntuaciones medias que obtiene un grupo de participantes en una variable (M₁) son diferentes de las puntuaciones medias que obtiene otro grupo de participantes en esa misma variable (M₂). La variable bajo estudio se denomina variable dependiente (VD), mientras que los grupos de comparación son la variable independiente (VI). Mediante un test de comparación de medias se resta la media de un grupo de la media del otro grupo, y se divide el resultado entre el error estándar de esa diferencia (esto es, se estandariza). Posteriormente se compara la diferencia estandarizada con una tabla de frecuencias de la que se obtiene el valor de probabilidad (o valor de p). Estadísticamente, el valor de p asociado a la diferencia estandarizada indica la probabilidad de encontrar una diferencia entre medias igual o más extrema que la encontrada si la hipótesis nula (de m₂ – m₁ = 0 en la población) es cierta¹⁷.

Sin embargo, el estadístico que está tomando mayor importancia frente al valor de p es el tamaño del efecto, el cual indica la magnitud de las diferencias con independencia de la significación estadística. El estadístico del tamaño del efecto más utilizado para la diferencia de medias es la d de Cohen¹⁸, el cual indica cuántas desviaciones típicas se desvía la media de un grupo respecto de la media del otro grupo. No obstante, se han calculado estimadores insesgados para muestras pequeñas¹⁹. Siguiendo las guías de Cohen, las diferencias de medias se interpretan como pequeñas, moderadas o grandes cuando el valor de d es igual o superior a 0.20, 0.50 y 0.80 respectivamente. Como indicador adicional, se puede conocer el porcentaje de solapamiento entre las distribuciones de puntuaciones en las dos muestras a partir del valor de la d de Cohen²⁰.

La importancia del tamaño del efecto es que indica si es interesante tomar en consideración la asociación entre variables. Por ejemplo, un tamaño del efecto demasiado grande podría indicar que esa variable diferencia suficientemente entre grupos y no es necesario incluirla como variable de estudio (p.ej., la diferencia de peso entre niños de 4 años y adultos de 30). Por su parte, un tamaño del efecto demasiado pequeño, o incluso insignificante, indica que la distribución de frecuencias entre los grupos se solapa tanto que no es útil para diferenciar entre los grupos (p.ej., la diferencia de peso entre personas de 20 años y personas de 22 años).

Como ejemplo, Garcia-Diaz y sus colaboradores²¹ administraron una tarea de velocidad de procesamiento de la información a una muestra de 20 personas mayores cognitivamente sanas [Media (M) = 46.90, Desviación Típica (DT) = 10.26] y a una muestra de 36 personas con Enfermedad de Parkinson (M = 32.60, DT = 22.04) y deterioro cognitivo leve. La VD es el número de ítems correctos tras 90 segundos. La prueba t para muestras independientes indica que la diferencia en las medias entre los dos grupos es estadísticamente significativa (t = 2.73, p = 0.008), lo que sugiere que las personas con Enfermedad de Parkinson y deterioro cognitivo leve identifican menos ítems en la misma prueba durante el mismo periodo de tiempo. La conclusión principal de este análisis es que las personas con Enfermedad de Parkinson y deterioro cognitivo leve presentan un enlentecimiento en la velocidad de procesamiento.

El estadístico d de Cohen para estos estadísticos es igual a 0.83, lo que indica un tamaño del efecto de moderado a grande. Asimismo, una d = 0.83 se asocia con un porcentaje de solapamiento de alrededor del 50%, lo que indica que aproximadamente el 50% de las puntuaciones en el grupo con Enfermedad de Parkinson está por debajo de la puntuación más baja observada en el grupo cognitivamente sano.

Es importante saber que aumentando los tamaños muestrales se reduce el error de medida y, por tanto, la desviación típica, lo cual tiene un impacto en el tamaño del efecto. Aunque la diferencia puede ir en cualquier dirección, el aumento del tamaño muestral suele estar asociado a una reducción del tamaño del efecto, lo que indica que los estadísticos del tamaño del efecto asociados a un valor de p menor de 0.05 y obtenidos en muestras pequeñas no son fiables, por lo que deben interpretarse con mucha cautela²².

Comparación de medias – Varios grupos

Cuando lo que se pretende es comparar las puntuaciones en una misma VD entre más de dos grupos, la prueba utilizada es el análisis de varianza (ANOVA) de un factor. En el ANOVA se cambia el término VI por el término factor, siendo el factor la variable relacionada con los grupos. En el ANOVA, la hipótesis nula es que todas las medias son iguales entre ellas (i.e., m₁ = m₂ = m_k, donde k es el número de grupos).

El ANOVA se basa en dos estimaciones de varianza²³. Por un lado, se analiza la varianza dentro de cada grupo, esto es, si las puntuaciones dentro de cada grupo son similares o presentan una marcada dispersión. Esta varianza intra-grupo se considera varianza aleatoria o varianza de error. Por otro lado, se analiza la diferencia entre medias de los grupos, lo que se considera un reflejo de la diferencia entre los grupos más el error. Si las dos estimaciones de varianza no difieren considerablemente, es decir, si la varianza entre-grupos es similar a la varianza intra-grupos, se concluye que todas las medias provienen de la misma distribución de medias y que cualquier pequeña diferencia se debe al error de muestreo. Por el contrario, si las medias de los grupos difieren más de lo esperable, se puede concluir que esas medias provienen de diferentes distribuciones y se rechaza la hipótesis nula de igualdad de medias²³. Sin embargo, el ANOVA que indica que las medias no son iguales entre los grupos no indica entre qué grupos existen diferencias. Para ello es necesario realizar pruebas adicionales.

En cuanto al tamaño del efecto relacionado con el ANOVA, el más utilizado es h² parcial (eta cuadrado parcial), que indica la varianza en la VD atribuible al efecto de interés más el error²³. El tamaño del efecto relacionado con h² parcial para cada variable independiente es de 0.010, 0.058 y 0.137 para un tamaño del efecto pequeño, moderado y grande respectivamente²⁴.

Como ejemplo, Smith, Dawes, Smith y Pal²⁵ compararon el procesamiento auditivo entre un grupo de 40 niños y adolescentes con epilepsia rolándica (G1), un grupo de 32 de los hermanos de los miembros del G1 (G2) y un grupo de 99 de los padres de los participantes del G1 (G3). Mediante escucha dicótica se presentaba una palabra en cada oído de manera simultánea, y se les solicitaba que repitieran la palabra que se les presentaba en uno u otro oído. Las puntuaciones (y su DT) de los grupos G1, G2 y G3 fue de 7.3 (3.8), 7.6 (3.7) y 8.9 (2.8) respectivamente. Los datos indican que la variabilidad dentro de los grupos es ligeramente inferior en el G3, y que las medias son similares entre los grupos G1 y G2. El ANOVA indica que la variabilidad entre las medias es superior a la esperable según la variabilidad debida al error de muestreo (F = 4.3, p = 0.015), con lo que se concluye que existen diferencias entre los grupos en la tarea de memoria. El ANOVA no permite conocer entre qué grupos ocurren las diferencias, pero pruebas post-hoc mostraron que los grupos G1 y G2 obtuvieron puntuaciones significativamente más bajas que el G3, sin diferencias entre los grupos G1 y G2. El estadístico h² parcial es de 0.38, lo que indica que el 38% de la varianza en la puntuación del test de escucha dicótica se asocia con la pertenencia a uno de los grupos.

Extensión del Análisis de Varianza – ANOVA de dos factores

Una de las particularidades del ANOVA es que es una técnica versátil que permite ampliar los análisis considerablemente. La primera extensión del ANOVA es la introducción de uno o más factores en el análisis. Así, el ANOVA permite analizar si las diferencias en la variable dependiente se deben a un factor, a otro factor o la interacción entre ambos. En el caso más simple se incluyen dos factores, lo que permite conocer dos efectos simples y un efecto de interacción. Los efectos simples indican si las diferencias en la VD se deben a los efectos de cada uno de los factores considerados de manera aislada. La interacción, por el contrario, indica si las diferencias entre los diferentes niveles de un factor se repiten en los diferentes niveles del otro factor²³.

Como ejemplo, Testa, Malec, Moessner y Brown²⁶ analizaron la relación entre la edad y el tipo de daño en la independencia en tareas relacionadas con el trabajo. Para ello, reclutaron a 195 personas con traumatismo craneoencefálico (TCE) y 82 personas con daño físico de tipo ortopédico. Los participantes de ambos grupos fueron, a su vez, separados en dos grupos de edad: de 18 a 49 años, y de 50 a 89 años. La VD en este estudio fue la puntuación en el cuestionario Vocational Independence Scale. Este diseño incluye dos factores: el factor Grupo (F1) y el factor Edad (F2). El análisis del factor simple F1 permite conocer si el rendimiento difiere, de manera general, entre personas con TCE y personas con daño ortopédico. Por otro lado, el análisis del factor simple F2 permite conocer si el rendimiento difiere, de manera general, en pacientes más mayores en comparación con pacientes más jóvenes.

Lo más interesante, sin embargo, es la interacción entre factores, que en este caso mostraría si uno de los grupos (F1) obtiene una puntuación diferente en función de la edad (F2). Los análisis mostraron un efecto principal del grupo (F = 20.30, p < 0.001) y un efecto principal de la edad (F = 8.02, p = 0.005). También se encontró una interacción significativa (F = 3.95, p = 0.048), indicando que las personas mayores que habían sufrido un TCE presentaban la menor independencia vocacional. Esta independencia vocacional era menor que la encontrada en las personas mayores con daño ortopédico y menor que las personas más jóvenes con independencia del daño que hubieran sufrido. Análisis de covarianza

La segunda ampliación del ANOVA es que permite incluir el efecto de una tercera variable, en este caso continua, en el análisis de la relación entre factores y la VD. Cuando se incluye una variable continua (denominada covariable) en un análisis de varianza, la nomenclatura cambia a Análisis de Covarianza (ANCOVA). En el ANCOVA, se analiza la relación entre factores y VD después de ajustar los valores de la VD en función de las diferencias en la covariable introducida (y que correlaciona con la VD)²³. Mediante el ANCOVA, se ajustan las medias de los grupos en la VD al valor que tomaría esta VD si todos los sujetos puntuaran igual en la covariable, por lo que las diferencias existentes se deben únicamente a los factores introducidos en el análisis (más otros desconocidos que no se han podido controlar). Esto indica que los efectos de la covariable en el ANCOVA se basan en una regresión lineal (ver más abajo).

Como ejemplo, Wobrock y sus colaboradores²⁷ compararon el rendimiento en tareas de funciones ejecutivas entre un grupo de 11 personas con primer episodio de esquizofrenia, 13 personas con esquizofrenia crónica, 18 personas con trastorno bipolar y 23 controles sanos. La VD es el número de intentos administrados en el Wisconsin Card Sorting Test (WCST). Para realizar el ANCOVA compararon la puntuación en el WCST ente los grupos controlando el sexo, la edad y el nivel educativo. En este ANCOVA introdujeron dos factores categóricos (grupo y sexo) y dos covariables (edad y nivel educativo). Los resultados mostraron que, controlando por edad, sexo y nivel educativo, existían diferencias significativas en el WCST, con el grupo de controles sanos realizando la tarea en un menor número de intentos (M = 88.45, DT = 16.77) en comparación con las personas con primer episodio de esquizofrenia (M = 110.91, DT = 18.56), las personas con esquizofrenia crónica (M =104.09, DT = 18.42) y las personas con trastorno bipolar (M = 103.25, DT = 20.92). Los autores no indicaron el efecto de la edad o el nivel educativo sobre la VD, por lo que no es posible conocer si las puntuaciones en el WCST disminuyeron en función de la edad o los años de escolaridad.

ANOVA de medidas repetidas

La tercera ampliación del ANOVA, y quizá de las más importantes para interpretar estudios sobre intervenciones cognitivas en personas con daño neurológico, es el análisis de una VD en varios momentos temporales (intra-sujetos), manteniendo la posibilidad de incluir tanto factores entre-sujetos como covariables. En este caso, denominado ANOVA de medidas repetidas (o ANOVA mixto si incluye factores entre-sujetos y factores intra-sujetos), se analizan tanto los efectos de los factores simples como la interacción entre factores, como se describe en la sección dedicada al ANOVA de dos factores. La diferencia fundamental entre el ANOVA de dos factores y el ANOVA de medidas repetidas es la independencia de los datos. En el ANOVA de dos factores entre-sujetos, cada factor incluye datos de dos grupos diferentes y, por tanto, independientes²³. En el caso del ANOVA de medidas repetidas, el factor intra-sujetos incluye valores obtenidos en los mismos sujetos en varios momentos diferentes (p.ej., antes y después de la intervención), por lo que los datos están relacionados entre sí y no son independientes.

Como ejemplo, De Simone, Perri, Fadda, Caltagirone y Carlesimo²⁸ analizaron el rendimiento de 80 personas con Deterioro Cognitivo Leve (DCL) y 62 controles sanos en una tarea de memoria verbal. El grupo DCL fue, a su vez, dividido en dos grupos: un grupo de 39 personas con DCL que progresaron a Enfermedad de Alzheimer y un grupo de 41 personas con DCL que se mantuvieron estables en un periodo de tres años. Este diseño incluyó una variable entre-sujetos con dos niveles (factor Grupo, F1) y una variable intra-sujetos (factor Tiempo, F2) con dos niveles: puntuaciones en la última serie de recuerdo inmediato vs. puntuaciones en el recuerdo diferido.

El ANOVA de medidas repetidas mostró un efecto principal del factor grupo (F = 79.03, p < 0.001), un efecto principal del factor tiempo (F = 330.8, p < 0.001), y una interacción significativa (F = 9.33, p < .001). En cuanto al factor grupo, los controles sanos obtuvieron en global puntuaciones superiores a los dos grupos con DCL, mientras que las personas con DCL que progresaron a Enfermedad de Alzheimer obtuvieron puntuaciones en global significativamente más bajas que las personas con DCL que se mantuvieron estables. En cuanto al factor tiempo, las puntuaciones en la última serie del recuerdo inmediato fueron, en general y contando con todos los grupos, mayores que las puntuaciones en el recuerdo diferido. Lo más importante en este diseño, sin embargo, es la interacción entre factores. La interacción entre grupo y tiempo mostró que las personas en los dos grupos con DCL mostraron una pérdida entre la última serie del recuerdo inmediato y la serie de recuerdo diferido similar (p = 0.07), significativamente más marcada que la encontrada en el grupo de controles sanos (ps < 0.001). Por lo tanto, la interacción significativa entre factores muestra que lo que ocurre en alguno de los grupos de un factor no ocurre en alguno de los grupos del otro factor. En un estudio de intervención, se escogen dos grupos de personas con patología neurológica. A uno de los grupos se le realiza una intervención cognitiva, mientras que el otro grupo no la recibe, y ambos grupos son evaluados con las mismas pruebas en los mismos momentos temporales (antes y después de la intervención en el grupo experimental). El investigador está interesado en encontrar una interacción significativa entre los factores grupo y tiempo, de manera que las puntuaciones en un grupo antes y después sean diferentes a las del otro grupo. Si el grupo sin intervención se mantiene estable, se espera que el grupo con intervención mejore; si el grupo sin intervención empeora, se espera que el grupo con intervención mejore o se mantenga estable. Análisis de asociación – Correlaciones

En ocasiones los investigadores están interesados en conocer si los cambios en una variable continua se relacionan con cambios en otra variable continua, dentro de un grupo. En este caso, los análisis de correlaciones bivariadas (dos variables) permiten conocer si el aumento o disminución en los valores de una variable se asocian con un aumento o una disminución en los valores de otra variable²³. Las correlaciones bivariadas más utilizadas en investigación son la r de Pearson, para variables que se distribuyen normalmente, y la Rho de Spearman para variables que no se distribuyen normalmente.

El estadístico de correlación puede tomar valores entre ±1. Los valores positivos indican que el aumento en los valores de una variable se asocia con el aumento en los valores de la otra variable. Los valores negativos de r indican que los valores de una variable disminuyen conforme aumentan los valores de la otra variable. Una correlación no significativa o con valores cercanos a 0 indica que no existe asociación entre variables y, por tanto, los cambios en una variable no tienen relación con los cambios en la otra variable.

El tamaño del efecto indica una asociación pequeña, moderada o grande para valores r = 0.10, r = 0.30 y r = 0.50 respectivamente¹⁸. Por otra parte, el cuadrado de la correlación (r²) indica la proporción de varianza en una variable explicada por la otra variable, y puede tomar valores entre 0 y 1. Cuanto mayor es la varianza explicada más cercano es r² a 1, mayor es la asociación entre variables y mejor pueden predecirse los valores de una variable en función de las puntuaciones en la otra variable²³. Es muy importante tener presente que, como en el caso de las diferencias de medias, los análisis de correlación indican asociación, pero en ningún caso causalidad.

Como ejemplo, Borghesani y sus colaboradores²⁹ analizaron la asociación entre la edad y la velocidad de procesamiento con otras variables cognitivas relacionadas con la memoria, la fluencia verbal, el razonamiento y la flexibilidad cognitiva en 165 personas mayores cognitivamente sanas. Sus resultados mostraron que la edad correlacionó de manera significativa con la velocidad de procesamiento (r = -0.36), la memoria (r = -0.24), la fluencia verbal (r = -0.15), el razonamiento (r = -0.43) y la flexibilidad cognitiva (r = -0.40). El signo negativo de las correlaciones indica que las puntuaciones en los diferentes tests cognitivos disminuía conforme aumentaba la edad. En cuanto a la velocidad de procesamiento, los resultados mostraron una asociación significativa con la memoria (r = 0.47), la fluencia verbal (r = 0.62), el razonamiento (r = 0.64) y la flexibilidad cognitiva (r = 0.34). El signo positivo de las correlaciones indica que las puntuaciones en los diferentes tests aumentaban conforme aumentaban las puntuaciones en tests de velocidad de procesamiento. Sin embargo, pese a la significación estadística, las medidas de tamaño del efecto indican que la relación entre variables es generalmente baja, explicando porcentajes de varianza entre el 2.25% y el 22%. Las asociaciones más importantes se encontraron entre la velocidad de procesamiento y la fluencia verbal (R² = 38.4%), por un lado, y la velocidad de procesamiento y el razonamiento por otro (R² = 41%).

Análisis de asociación – Regresión lineal

Los análisis de correlación indican la asociación entre dos variables continuas, esto es, cómo los cambios en una variable afectan a otra variable. Si dos variables están relacionadas se puede predecir, con cierto grado de confianza, los valores de una variable en función de los valores de la otra variable. Este análisis de predicción se realiza a través de análisis de regresión³⁰. Cuando la variable dependiente que se quiere predecir, denominada criterio, es una variable continua el análisis adecuado es la regresión lineal. Las variables independientes utilizadas para predecir la variable criterio, denominadas predictores, pueden ser variables categóricas y variables continuas.

Los análisis de regresión se utilizan para responder a dos cuestiones generales de investigación³⁰. En primer lugar, aportan información acerca de la asociación de variables. Si se utiliza una variable dicotómica como predictor de una variable continua, el coeficiente asociado al predictor es igual al que se obtendría con un análisis de diferencia de medias. En segundo lugar, los coeficientes obtenidos en los análisis de regresión son útiles para predecir los valores de la variable criterio a partir de los valores del conjunto de variables predictoras.

Dos son los estadísticos más relevantes para los investigadores en un análisis de regresión lineal. Los estadísticos relacionados con cada predictor se denominan coeficientes, e indican el cambio medio en la variable criterio por cada aumento de una unidad en la variable predictora. Cuando hay dos o más predictores, el coeficiente de cada predictor indica el cambio medio en la variable criterio por cada aumento de una unidad en el predictor manteniendo el resto de predictores constantes. El segundo estadístico relevante es R², que indica el porcentaje de varianza de la variable criterio que se explica por la combinación de predictores. R² puede tomar valores entre 0 y 1. Los valores más cercanos a 1 indican una relación absoluta entre predictores y criterio, mientras valores cercanos a 0 indican que no existe asociación entre la variable criterio y los predictores. R² es útil para calcular el tamaño del efecto del modelo, con valores de 0.02, 0.13 y 0.26 indicando un tamaño del efecto pequeño, moderado y grande respectivamente¹⁸.

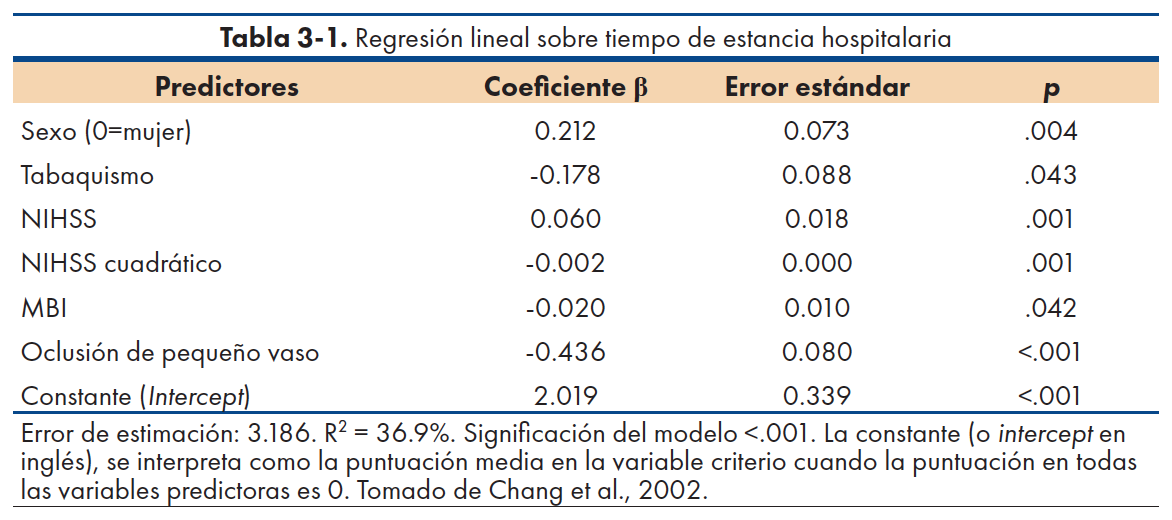
Como ejemplo, Chang y sus colaboradores³¹ analizaron el tiempo de estancia hospitalaria en 330 pacientes con primer ictus isquémico. Con el fin de identificar variables relacionadas con el tiempo de estancia recogieron datos sobre el sexo del paciente, la edad, la gravedad del ictus, independencia funcional, tiempo pasado desde el ictus (<24h o >24h), comorbilidad (hipertensión, diabetes mellitus, hipercolesterolemia), tabaquismo, problemas cardiacos, subtipo de ictus (oclusión de pequeño vaso o no), y niveles de colesterol y triglicéridos. La gravedad del ictus se analizó mediante la escala National Institutes of Health Stroke Scale (NIHSS), con un rango de 0 a 38 y mayores puntuaciones indicando mayor gravedad. La independencia funcional se analizó mediante el Índice de Barthel Modificado (rango 0-20), en el que mayores puntuaciones indican mayor independencia funcional. La variable dependiente en el análisis de regresión fue el tiempo de estancia (en valores logarítmicos), con el que los autores pretendían conseguir la normalidad de la distribución de los datos. Aunque no es el objetivo del presente trabajo, esta transformación indica que los autores malinterpretaron los supuestos del análisis de regresión. Según el Modelo Lineal General son los residuos, y no las variables, quienes deben distribuirse normalmente³².

Los resultados indicaron que el tiempo medio de estancia fue de 11 días (DT = 14). La mayoría de los pacientes (62%) sufrió un ictus por oclusión de pequeño vaso, seguido de aterosclerosis (25%) y cardioembolismo (12%). La mayoría de los pacientes (81%) ingresó dentro de las primeras 24 horas tras el ictus. De los 330 pacientes, 17 (5%) murieron durante la hospitalización aguda, 86 (26%) fueron trasladados al servicio de rehabilitación intensiva, y 227 (69%) fueron dados de alta y regresaron a su residencia habitual u otros servicios de atención médica.

Los datos del análisis de regresión se presentan en la tabla 1. El tiempo de estancia aumentó en hombres respecto a mujeres, en no-fumadores respecto a fumadores, en los casos con mayor gravedad, en casos con mayor dependencia funcional y en los casos con tipo de ictus diferente a la oclusión de pequeño vaso.

Sin embargo, lo relevante de los análisis de regresión es que no solo indican si existe una relación estadísticamente significativa, sino que aportan la posibilidad de conocer cuál es la asociación de cada predictor con la variable criterio controlando el resto de predictores. En el ejemplo de la tabla 1 se observa que los hombres presentan una estancia media 1.24 días superior que las mujeres cuando se controlan los demás predictores. Respecto a la historia de tabaquismo, la estancia media se reduce de media en 0.84 días en los fumadores respecto a los no-fumadores.

Además de la asociación entre predictores y variable criterio, los análisis de regresión permiten predecir los valores de la variable criterio a partir de los diferentes valores de los predictores. En el caso del ejemplo de la tabla 1, se podría predecir la estancia hospitalaria con la fórmula

donde es la puntuación predicha para el sujeto i, es el coeficiente de la variable j, es la puntuación del sujeto i en la variable j, y es el error. Utilizando los valores de la tabla 1, la predicción del tiempo de estancia hospitalaria para un varón fumador con una puntuación NIHSS=10, una puntuación en el Índice de Barthel=15, y diagnóstico de ictus por oclusión de pequeño vaso sería:

Puesto que la variable criterio era el logaritmo del tiempo de estancia, hay que invertir el valor del logaritmo (e^1.717), lo cual indica que la estancia hospitalaria en este paciente ascendería a 5.57 días.

Las diferencias entre los valores reales y los valores predichos por el modelo de regresión en cada individuo se conocen como residuos, e indican si las predicciones del modelo son adecuadas. Cuanto mayores son los residuos, menor es la capacidad predictora del modelo y mayor es el error²³. Es importante que los investigadores tengan en cuenta que, en los análisis de regresión, el análisis de residuos es esencial para comprobar la adecuación del modelo. Aunque el tamaño de la muestra no modifica los coeficientes asociados a cada predictor, las muestras pequeñas se asocian con mayores residuos y, por tanto, un mayor error de la predicción, lo cual puede llegar a invalidar la utilidad para predecir la variable criterio con esos predictores^32,33.